Nonlinearity

Various definitions of an attractor for a nonlinear dynamical system have been proposed. These use various assumptions on the set of initial conditions that should converge (the basin), and various notions of convergence. A weak assumption on the basin is the measure attractor of Milnor, which requires that the basin has positive measure. A weak assumption of the notion of convergence is the statistical attractor due to Ilyashenko, which requires that limiting to the attractor occurs on a set of future times of full density. We point out that many examples of statistical attractors actually satisfy a stronger definition which we call a bounded-return-time attractor, and we investigate such attractors. We also give an improved definition for the notion of pullback measure attraction. This was originally developed to understand attractors in nonautonomous systems, but we note here that it is helpful for understanding convergence towards statistical attractors in the autonomous setting. We investigate implications between all these different notions of attractors. We also investigate which of these notions are fulfilled by a hyperbolic fixed point with a homoclinic loop.

This paper considers a susceptible-infected-susceptible epidemic reaction-diffusion model with no-flux boundary conditions and varying total population. The interaction of the susceptible and infected people is described by the nonlinear transmission mechanism of the form $S^qI^p$, where $0 \lt p\unicode{x2A7D} 1$ and q > 0. In Peng et al (SIAM J. Math. Anal. (arXiv:2411.00582)), we have studied a model with a constant total population. In the current paper, we extend our analysis to a model with a varying total population, incorporating birth and death rates. We investigate the asymptotic profiles of the endemic equilibrium when the dispersal rates of susceptible and/or infected individuals are small. Our work is motivated by disease control strategies that limit population movement. To illustrate the main findings, we conduct numerical simulations and provide a discussion of the theoretical results from the view of disease control. We will also compare the results for the models with constant or varying total population.

We establish the optimal convergence rate of the hypersonic similarity for two-dimensional steady potential flows with large data past a straight wedge in the 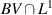$BV\cap L^1$ framework, provided that the total variation of the large data multiplied by 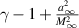$\gamma-1+\frac{a_{\infty}^2}{M_\infty^2}$ is uniformly bounded with respect to the adiabatic exponent γ > 1, the Mach number 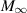$M_\infty$ of the incoming steady flow, and the hypersonic similarity parameter 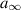$a_\infty$. Our main approach in this paper is first to establish the well-posedness and the Lipschitz continuous map $\mathcal{P}$ that has the properties similar to the Standard Riemann Semigroup of the initial-boundary value problem for the isothermal hypersonic small disturbance equations with large data, and then to compare the Riemann solutions between two systems with boundary locally case by case. Based on them, we derive the global L¹–estimate between the two solutions by employing the Lipschitz continuous map 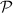$\mathcal{P}$ and the local L¹–estimates. We further construct an example to show that the convergence rate is optimal.

In many situations, the combined effect of advection and diffusion greatly increases the rate of convergence to equilibrium—a phenomenon known as enhanced dissipation. Here we study the situation where the advecting velocity field generates a random dynamical system satisfying certain Harris conditions. If κ denotes the strength of the diffusion, then we show that with probability at least $1 - o(\kappa^N)$ enhanced dissipation occurs on time scales of order $\vert \ln \kappa \rvert$, a bound which is known to be optimal. Moreover, on long time scales, we show that the rate of convergence to equilibrium is almost surely independent of diffusivity. As a consequence we obtain enhanced dissipation for the randomly shifted alternating shears introduced by Pierrehumbert'94.

In this article, we present a comprehensive framework for constructing smooth, localized solutions in systems of semi-linear partial differential equations, with a particular emphasis to the Gray–Scott model. Specifically, we construct a natural Hilbert space 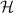$\mathcal{H}$ for the study of systems of autonomous semi-linear PDEs, on which products and differential operators are well-defined. Then, given an approximate solution u₀, we derive a Newton–Kantorovich approach based on the construction of an approximate inverse of the linearization around u₀. In particular, we derive a condition under which we prove the existence of a unique solution in a neighborhood of u₀. Such a condition can be verified thanks to the explicit computation of different upper bounds, for which analytical details are presented. Furthermore, we provide an extra condition under which localized patterns are proven to be the limit of an unbounded branch of (spatially) periodic solutions as the period tends to infinity. We then demonstrate our approach by proving (constructively) the existence of four different localized patterns in the 2D Gray–Scott model. In addition, these solutions are proven to satisfy the D₄-symmetry. That is, the symmetry of the square. The algorithmic details to perform the computer-assisted proofs are available on GitHub (2024 LocalizedPatternsGS.jl https://github.com/dominicblanco/LocalizedPatternsGS.jl).

It is a well known fact that the geometry of a superconducting sample influences the distribution of the surface superconductivity for strong applied magnetic fields. For instance, the presence of corners induces geometric terms described through effective models in sector-like regions. We study the connection between two effective models for the offset of superconductivity and for surface superconductivity introduced in Bonnaillie-Noël and Fournais (2007 Rev. Math. Phys. 19 607–37) and Correggi and Giacomelli (2021 Calc. Var. PDE 60 236), respectively. We prove that the transition between the two models is continuous with respect to the magnetic field strength, and, as a byproduct, we deduce the existence of a minimizer at the threshold for both effective problems. Furthermore, as a consequence, we disprove a conjecture stated in Correggi and Giacomelli (2021 Calc. Var. PDE 60 236) concerning the dependence of the corner energy on the angle close to the threshold.

We obtain rigorous large time asymptotics for the Landau–Lifshitz (LL) equation in the soliton free case by extending the nonlinear steepest descent method to genus 1 surfaces. The methods presented in this paper pave the way to a rigorous analysis of other integrable equations on the torus and enable asymptotic analysis on different regimes of the LL equation.

We develop a system of non-linear stochastic evolution equations that describes the continuous measurements of quantum systems with mixed initial state. We address quantum systems with unbounded Hamiltonians and unbounded interaction operators. Using arguments of the theory of quantum measurements we derive a system of stochastic interacting wave functions (SIWFs for short) that models the continuous monitoring of quantum systems. We prove the existence and uniqueness of the solution to this system under conditions general enough for the applications. We obtain that the mixed state generated by the SIWF at any time does not depend on the initial state, and satisfies the diffusive stochastic quantum master equation, which is also known as Belavkin equation. We present two physical examples. In one, the SIWF becomes a system of non-linear stochastic partial differential equations. In the other, we deal with a model of a circuit quantum electrodynamics.

We investigate the metric mean dimension of subshifts of compact type. We prove that the metric mean dimensions of a continuous map and its inverse limit coincide, generalizing Bowen's entropy formula. Building upon this result, we extend the notion of metric mean dimension to discontinuous maps in terms of suitable subshifts. As an application, we show that the metric mean dimension of the Gauss map and that of induced maps of the Manneville–Pomeau family is equal to the box dimension of the corresponding set of discontinuity points, which also coincides with a critical parameter of the pressure operator associated to the geometric potential.

For countably infinite IFSs on $\mathbb{R}^2$ consisting of affine contractions with diagonal linear parts, we give conditions under which the affinity dimension is an upper bound for the Hausdorff dimension and a lower bound for the lower box-counting dimension. Moreover, we identify a family of countably infinite IFSs for which the Hausdorff and the affinity dimension are equal, and which have full dimension spectrum. The corresponding self-affine sets are related to restricted digit sets for signed Lüroth expansions.

In this paper, we study the well-posedness of classical solutions to a two-phase flow model consisting of the pressureless Euler equations coupled with the isentropic compressible Navier–Stokes equations via a drag forcing term. We consider the case that the fluid densities may contain a vacuum, and the viscosities are density-dependent functions. Under suitable assumptions on the initial data, we show that the finite-energy (i.e. in the inhomogeneous Sobolev space) classical solutions to the Cauchy problem of this coupled system do not exist for any small time.

We investigate the relationship between rigid motions and relative equilibria in the N-body problem on the two-dimensional sphere, $\mathbb{S}^2$. We prove that any rigid motion of the N-body system on $\mathbb{S}^2$ must be a relative equilibrium. Our approach extends the classical study of rigid body dynamics and utilizes a rotating frame attached to the particles to derive the corresponding equations of motion. We further show that our results can be extended to the N-body gravitational system in $\mathbb{R}^3$. The results are oriented to a broader understanding of the dynamics of N-body systems on curved surfaces.

A nonautonomous periodic chemostat model with delays modelling n species in competition is considered. Sufficient conditions on the coefficients and consumption functions for the species are given, for both the extinction of the species and for the existence of n nontrivial and nonnegative periodic solutions. Further criteria guarantee that the system admits at least one strictly positive periodic solution.

In this article we study the well-posedness of the generalized derivative nonlinear Schrödinger equation (gDNLS) $iu_t+u_{xx} = i|u|^{2\sigma}u_x,$ for small powers σ. We analyze this equation at both low and high regularity, and are able to establish global well-posedness in H^s when $s \in [1,4\sigma)$ and $\sigma \in (\frac{\sqrt{3}}{2},1)$. Our result when s = 1 is particularly relevant because it corresponds to the regularity of the energy for this problem. Moreover, a theorem of Liu et al (2013 J. Nonlinear Sci.23 557–83) establishes the orbital stability of the gDNLS solitons, provided that there is a suitable H¹ well-posedness theory. To our knowledge, this is the first low regularity well-posedness result for a quasilinear dispersive model where the nonlinearity is both rough and lacks the decay necessary for global smoothing type estimates. These two features pose considerable difficulty when trying to apply standard tools for closing low-regularity estimates. While the tools developed in this article are used to study gDNLS, we believe that they should be applicable in the study of local well-posedness for other dispersive equations of a similar character. It should also be noted that the high regularity well-posedness presents a novel issue, as the roughness of the nonlinearity limits the potential regularity of solutions. Our high regularity well-posedness threshold $s \lt 4\sigma$ is twice as high as one might naïvely expect, given that the function $z \mapsto |z|^{2\sigma}$ is only $C^{1,2\sigma-1}$ Hölder continuous. Moreover, although we cannot prove H¹ well-posedness when $\sigma \unicode{x2A7D} \frac{\sqrt{3}}{2}$, we are able to establish H^s well-posedness in the high regularity regime $s \in (2-\sigma,4\sigma)$ for the full range of $\sigma \in (\frac{1}{2},1)$. This considerably improves the known local results, which had only been established in either H² or in weighted Sobolev spaces.

We consider the system of viscoelasticity with higher-order gradients and nonconvex energy in several space dimensions. We establish the asymptotic limits when the viscosity $\nu\rightarrow 0$ or when the dispersion coefficient $\delta \rightarrow 0$. For the latter problem, it is worth noting that, for the case of two space dimensions, we also establish a rate of convergence. This result bears analogies to a result of Chemin (1996 Commun. PDE21 1771–79) on the rate of convergence of the zero-viscosity limit for the two-dimensional Navier–Stokes equations with bounded vorticity.

Pattern forming systems allow for a wealth of states, where wavelengths and orientation of patterns varies and defects disrupt patches of monocrystalline regions. Growth of patterns has long been recognized as a strong selection mechanism. We present here recent and new results on the selection of patterns in situations where the pattern-forming region expands in time. The wealth of phenomena is roughly organised in bifurcation diagrams that depict wavenumbers of selected crystalline states as functions of growth rates. We show how a broad set of mathematical and numerical tools can help shed light into the complexity of this selection process.

In this survey we recall basic notions of disintegration of measures and entropy along unstable laminations. We review some roles of unstable entropy in smooth ergodic theory including the so-called invariance principle, Margulis construction of measures of maximal entropy, physical measures and rigidity. We also give some new examples and pose some open problems.

This article is firstly a historic review of the theory of Riemann–Hilbert problems with particular emphasis placed on their original appearance in the context of Hilbert's 21st problem and Plemelj's work associated with it. The secondary purpose of this note is to invite a new generation of mathematicians to the fascinating world of Riemann–Hilbert techniques and their modern appearances in nonlinear mathematical physics. We set out to achieve this goal with six examples, including a new proof of the integro-differential Painlevé-II formula of Amir et al (2011 Commun. Pure Appl. Math.64 466–537) that enters in the description of the Kardar–Parisi–Zhang crossover distribution. Parts of this text are based on the author's Szegő prize lecture at the 15th International Symposium on Orthogonal Polynomials, Special Functions and Applications (OPSFA) in Hagenberg, Austria.

For a wide range of values of the intensity of the incoming solar radiation, the Earth features at least two attracting states, which correspond to competing climates. The warm climate is analogous to the present one; the snowball climate features global glaciation and conditions that can hardly support life forms. Paleoclimatic evidences suggest that in the past our planet flipped between these two states. The main physical mechanism responsible for such an instability is the ice-albedo feedback. In a previous work, we defined the Melancholia states that sit between the two climates. Such states are embedded in the boundaries between the two basins of attraction and feature extensive glaciation down to relatively low latitudes. Here, we explore the global stability properties of the system by introducing random perturbations as modulations to the intensity of the incoming solar radiation. We observe noise-induced transitions between the competing basins of attraction. In the weak-noise limit, large deviation laws define the invariant measure, the statistics of escape times, and typical escape paths called instantons. By constructing the instantons empirically, we show that the Melancholia states are the gateways for the noise-induced transitions. In the region of multistability, in the zero-noise limit, the measure is supported only on one of the competing attractors. For low (high) values of the solar irradiance, the limit measure is the snowball (warm) climate. The changeover between the two regimes corresponds to a first-order phase transition in the system. The framework we propose seems of general relevance for the study of complex multistable systems. Finally, we put forward a new method for constructing Melancholia states from direct numerical simulations, which provides a possible alternative with respect to the edge-tracking algorithm.

We review here the derivation of many of the most important models that appear in the literature (mainly in coastal oceanography) for the description of waves in shallow water. We show that these models can be obtained using various asymptotic expansions of the 'turbulent' and non-hydrostatic terms that appear in the equations that result from the vertical integration of the free surface Euler equations. Among these models are the well-known nonlinear shallow water (NSW), Boussinesq and Serre–Green–Naghdi (SGN) equations for which we review several pending open problems. More recent models such as the multi-layer NSW or SGN systems, as well as the Isobe–Kakinuma equations are also reviewed under a unified formalism that should simplify comparisons. We also comment on the scalar versions of the various shallow water systems which can be used to describe unidirectional waves in horizontal dimension d  =  1; among them are the KdV, BBM, Camassa–Holm and Whitham equations. Finally, we show how to take vorticity effects into account in shallow water modeling, with specific focus on the behavior of the turbulent terms. As examples of challenges that go beyond the present scope of mathematical justification, we review recent works using shallow water models with vorticity to describe wave breaking, and also derive models for the propagation of shallow water waves over strong currents.

A nonautonomous periodic chemostat model with delays modelling n species in competition is considered. Sufficient conditions on the coefficients and consumption functions for the species are given, for both the extinction of the species and for the existence of n nontrivial and nonnegative periodic solutions. Further criteria guarantee that the system admits at least one strictly positive periodic solution.

In this article we study the well-posedness of the generalized derivative nonlinear Schrödinger equation (gDNLS) $iu_t+u_{xx} = i|u|^{2\sigma}u_x,$ for small powers σ. We analyze this equation at both low and high regularity, and are able to establish global well-posedness in H^s when $s \in [1,4\sigma)$ and $\sigma \in (\frac{\sqrt{3}}{2},1)$. Our result when s = 1 is particularly relevant because it corresponds to the regularity of the energy for this problem. Moreover, a theorem of Liu et al (2013 J. Nonlinear Sci.23 557–83) establishes the orbital stability of the gDNLS solitons, provided that there is a suitable H¹ well-posedness theory. To our knowledge, this is the first low regularity well-posedness result for a quasilinear dispersive model where the nonlinearity is both rough and lacks the decay necessary for global smoothing type estimates. These two features pose considerable difficulty when trying to apply standard tools for closing low-regularity estimates. While the tools developed in this article are used to study gDNLS, we believe that they should be applicable in the study of local well-posedness for other dispersive equations of a similar character. It should also be noted that the high regularity well-posedness presents a novel issue, as the roughness of the nonlinearity limits the potential regularity of solutions. Our high regularity well-posedness threshold $s \lt 4\sigma$ is twice as high as one might naïvely expect, given that the function $z \mapsto |z|^{2\sigma}$ is only $C^{1,2\sigma-1}$ Hölder continuous. Moreover, although we cannot prove H¹ well-posedness when $\sigma \unicode{x2A7D} \frac{\sqrt{3}}{2}$, we are able to establish H^s well-posedness in the high regularity regime $s \in (2-\sigma,4\sigma)$ for the full range of $\sigma \in (\frac{1}{2},1)$. This considerably improves the known local results, which had only been established in either H² or in weighted Sobolev spaces.

We consider the system of viscoelasticity with higher-order gradients and nonconvex energy in several space dimensions. We establish the asymptotic limits when the viscosity $\nu\rightarrow 0$ or when the dispersion coefficient $\delta \rightarrow 0$. For the latter problem, it is worth noting that, for the case of two space dimensions, we also establish a rate of convergence. This result bears analogies to a result of Chemin (1996 Commun. PDE21 1771–79) on the rate of convergence of the zero-viscosity limit for the two-dimensional Navier–Stokes equations with bounded vorticity.

We study a fuzzy Boltzmann equation, where particles interact via delocalised collisions, in contrast to classical Boltzmann equations. We discuss the existence and uniqueness of solutions and provide a natural variational characterisation by casting the fuzzy Boltzmann equation into the framework of GENERIC systems (General Equations for Non-Equilibrium Reversible-Irreversible Coupling).

We study curvatures of the groups of measure-preserving diffeomorphisms of non-orientable compact surfaces. For the cases of the Klein bottle and the real projective plane we compute curvatures, their asymptotics and the normalised Ricci curvatures in many directions. Extending the approach of Arnold and Lukatskii we provide estimates of weather unpredictability for natural models of trade wind currents on the Klein bottle and the projective plane.

In this paper we prove an abstract result of almost global existence for small and smooth solutions of some semilinear PDEs on Riemannian manifolds with globally integrable geodesic flow. Some examples of such manifolds are Lie groups (including flat tori), homogeneous spaces and rotational invariant surfaces. As applications of the abstract result we prove almost global existence for a nonlinear Schrödinger equation with a convolution potential and for a nonlinear beam equation. We also prove H^s stability of the ground state in NLS equation. The proof is based on a normal form procedure and the combination of the arguments used in Bambusi and Langella (2022 arXiv:2202.04505) to bound the growth of Sobolev norms in linear systems and a generalization of the arguments in Bambusi et al (2024 Commun. Math. Phys.405 253–85).

We consider a one-dimensional system of four inelastic hard spheres, colliding with a fixed restitution coefficient r, and we study the inelastic collapse phenomenon for such a particle system. We study a periodic, asymmetric collision pattern, proving that it can be realized, despite its instability. We prove that we can associate to the four-particle dynamical system another dynamical system of smaller dimension, acting on $\{1,2,3\} \times \mathbb{S}^2$, and that encodes the collision orders of each trajectory. We provide different representations of this new dynamical system, and study numerically its ω-limit sets. In particular, the numerical simulations suggest that the orbits of such a system might be quasi-periodic.

This paper considers an SIS model with a cross-diffusion dispersal strategy for the infected individuals describing the public health intervention measures (like quarantine) during the outbreak of infectious diseases. The model adopts the frequency-dependent transmission mechanism and includes demographic changes (i.e. population recruitment and death) subject to homogeneous Neumann boundary conditions. We first establish the existence of global classical solutions with the uniform-in-time bound. Then, we define the basic reproduction number R₀ by a weighted variational form. Due to the presence of the cross-diffusion on infected individuals, we employ a change of variable and apply the index theory along with the principal eigenvalue theory to establish the threshold dynamics in terms of R₀ based on the fact that the sign of the principal eigenvalue of the weighted eigenvalue problem is the same as that of the corresponding unweighted eigenvalue problem. Furthermore, we obtain the global stability of the unique disease-free equilibrium and constant endemic equilibrium under some conditions. Finally, we discuss some open questions and use numerical simulation to demonstrate the applications of our analytical results, showing that the cross-diffusion dispersal strategy can reduce the value of R₀ and help eradicate the diseases even if the habitat is high-risk in contrast to the situation without cross-diffusion.

We initiate the mathematical study of the Bistritzer–MacDonald Hamiltonian for twisted trilayer graphene in the chiral limit (and beyond). We develop a spectral theoretic approach to investigate the presence of flat bands under specific magic parameters. This allows us to derive trace formulae that show that the tunneling parameters that lead to flat bands are nowhere continuous as functions of the twisting angles.

We prove extreme value laws for cusp excursions of the horocycle flow in the case of surfaces of constant negative curvature. The key idea of our approach is to study the hitting time distribution for shrinking Poincaré sections that have a particularly simple scaling property under the action of the geodesic flow. This extends the extreme value law of Kirsebom and Mallahi-Karai (2022 arXiv:2209.07283) for cusp excursions for the modular surface. Here we show that the limit law can be expressed in terms of Hall's formula for the gap distribution of the Farey sequence.